Biologist Finds New Solution to a 60-Year Old Math Problem

A new solution has been found for a half-a-century old math problem by an unlikely pioneer, Aubrey de Grey, a biologist who works on anti-ageing technologies. The problem was proposed by Edward Nelson in 1950. He said, assume there is a graph on a 2D plane — a set of points and lines, some of which may be interconnected, and all the points are at the same distance from each other. Then, if we started colouring the points, what is the least number of colours required so that no two adjacent points are of the same colour?

This came to be known as the Hadwiger-Nelson problem. It is essentially a chromatic number problem extended to an infinite number of points.

Plane graphs.

Vertex colouring and chromatic number

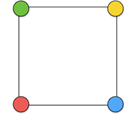
If we look at a finite graph, which can be as simple as the square above, it has four points and lines connected with each other.

The chromatic number of this graph is the least number of colours required so no two connected points are of the same colour.

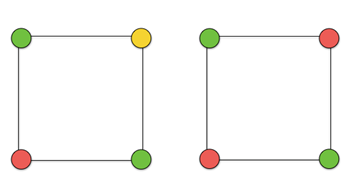
Chromatic number 3.                  Chromatic number 2.

This can be done using three colours. But it can also be done using two. So the chromatic number becomes two.

Now, if we extend this problem to an infinite number of points, but with all the points being at a unit distance from each other, it becomes the Hadwiger-Nelson problem.

The Solution

Soon after the problem was formulated, researchers found the upper and lower bounds for it. It was discovered that at least four colours will be required for colouring an infinite unit-distance graph, and a maximum of seven colours can be used. 

The lower bound was found with the discovery of the Golomb graph around 1960-1965, by Golomb. 

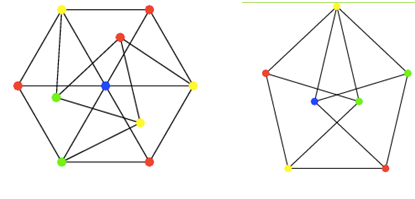
Golomb graph.                                     Moser spindle.

The other graph that illustrated the lower bound to this problem was the Moser spindle.

Both these graphs have a chromatic number of 4. Until now, all extensions of these graphs, i.e., addition of any new points, did not create the need for a new colour. Thus, as the number of colours required still remained at 4, it was established that chromatic number for a plane is 4.

50 years on, a different solution

Now, around 50 years after the Golomb graph was discovered, de Grey has found a graph that cannot be coloured using just 4 colours. De Grey’s graph has 1,581 vertices, and needs at leat five colours.

De Grey created this graph by fusing together multiple copies of the Moser spindle until it had 20,425 vertices and could not be coloured using 4 colours. He then embarked on the process of shrinking the graph, and was able to bring it down to 1,581 vertices while still needing five colours.

De Grey's graph.

Thus, now we know that the chromatic number for a plane is at least 5. With the analysis of bigger graphs, it is possible that the number could go even higher.

After de Grey posted his findings in a paper on arxiv.org, researchers became curious to see if the number of vertices in the graph could be reduced even further while still needing five colours. De Grey also got together with Terence Tao, a mathematician at the University of California, to post the problem of the reduction of vertices of Grey’s graph on Polymath.

Polymath is a 10 year old online platform that facilitates online collaborative work on mathematics problems. Soon after the problem was shared, new graphs were found having a smaller number of vertices and requiring 5 colours. The latest one was shared on Saturday by Marjin Heule, a computer scientist at University of Texas. Hueule’s graph lowered the number of vertices to 826.

Heule's graph.

Sixty years later, new solutions to this curious and deceptively simple problem are still being discovered. And there is still scope for something different.